Space and Time Complexity

Space complexity refers to the amount of memory used by an algorithm to complete its execution, as a function of the size of the input. The space complexity of an algorithm can be affected by various factors such as the size of the input data, the data structures used in the algorithm, the number and size of temporary variables, and the recursion depth. Time complexity refers to the amount of time required by an algorithm to run as the input size grows. It is usually measured in terms of the "Big O" notation, which describes the upper bound of an algorithm's time complexity.

Why do you think a programmer should care about space and time complexity?

  • the space and time will impact the programmer in many ways. the programmer should know what is the most efficient and most beneficial algorithm.

Take a look at our lassen volcano example from the data compression tech talk. The first code block is the original image. In the second code block, change the baseWidth to rescale the image.

from IPython.display import Image, display
from pathlib import Path 

# prepares a series of images
def image_data(path=Path("images/"), images=None):  # path of static images is defaulted
    for image in images:
        # File to open
        image['filename'] = path / image['file']  # file with path
    return images

def image_display(images):
    for image in images:  
        display(Image(filename=image['filename']))

if __name__ == "__main__":
    lassen_volcano = image_data(images=[{'source': "Peter Carolin", 'label': "Lassen Volcano", 'file': "lassen-volcano.jpg"}])
    image_display(lassen_volcano)
    

from IPython.display import HTML, display
from pathlib import Path 
from PIL import Image as pilImage 
from io import BytesIO
import base64

# prepares a series of images
def image_data(path=Path("images/"), images=None):  # path of static images is defaulted
    for image in images:
        # File to open
        image['filename'] = path / image['file']  # file with path
    return images

def scale_image(img):
    #baseWidth = 625
    #baseWidth = 1250
    #baseWidth = 2500
    baseWidth = 5000 # see the effect of doubling or halfing the baseWidth 
    #baseWidth = 10000 
    #baseWidth = 20000
    #baseWidth = 40000
    scalePercent = (baseWidth/float(img.size[0]))
    scaleHeight = int((float(img.size[1])*float(scalePercent)))
    scale = (baseWidth, scaleHeight)
    return img.resize(scale)

def image_to_base64(img, format):
    with BytesIO() as buffer:
        img.save(buffer, format)
        return base64.b64encode(buffer.getvalue()).decode()
    
def image_management(image):  # path of static images is defaulted        
    # Image open return PIL image object
    img = pilImage.open(image['filename'])
    
    # Python Image Library operations
    image['format'] = img.format
    image['mode'] = img.mode
    image['size'] = img.size
    image['width'], image['height'] = img.size
    image['pixels'] = image['width'] * image['height']
    # Scale the Image
    img = scale_image(img)
    image['pil'] = img
    image['scaled_size'] = img.size
    image['scaled_width'], image['scaled_height'] = img.size
    image['scaled_pixels'] = image['scaled_width'] * image['scaled_height']
    # Scaled HTML
    image['html'] = '<img src="data:image/png;base64,%s">' % image_to_base64(image['pil'], image['format'])


if __name__ == "__main__":
    # Use numpy to concatenate two arrays
    images = image_data(images = [{'source': "Peter Carolin", 'label': "Lassen Volcano", 'file': "lassen-volcano.jpg"}])
    
    # Display meta data, scaled view, and grey scale for each image
    for image in images:
        image_management(image)
        print("---- meta data -----")
        print(image['label'])
        print(image['source'])
        print(image['format'])
        print(image['mode'])
        print("Original size: ", image['size'], " pixels: ", f"{image['pixels']:,}")
        print("Scaled size: ", image['scaled_size'], " pixels: ", f"{image['scaled_pixels']:,}")
        
        print("-- original image --")
        display(HTML(image['html']))

Do you think this is a time complexity or space complexity or both problem?

  • This is both time and space complexity because the number of pixels is taking up space and the amount of time it takes for the program to run will increase as the basewidth changes.

Big O Notation

  • Constant O(1)
  • Linear O(n)
  • Quadratic O(n^2)
  • Logarithmic O(logn)
  • Exponential (O(2^n))
numbers = list(range(1000))
print(numbers)

Constant O(1)

Time

An example of a constant time algorithm is accessing a specific element in an array. It does not matter how large the array is, accessing an element in the array takes the same amount of time. Therefore, the time complexity of this operation is constant, denoted by O(1).

print(numbers[263])

ncaa_bb_ranks = {1:"Alabama",2:"Houston", 3:"Purdue", 4:"Kansas"}
#look up a value in a dictionary given a key
print(ncaa_bb_ranks[1])

Space

This function takes two number inputs and returns their sum. The function does not create any additional data structures or variables that are dependent on the input size, so its space complexity is constant, or O(1). Regardless of how large the input numbers are, the function will always require the same amount of memory to execute.

def sum(a, b): 
  return a + b

print(sum(90,88))
print(sum(.9,.88))

Linear O(n)

Time

An example of a linear time algorithm is traversing a list or an array. When the size of the list or array increases, the time taken to traverse it also increases linearly with the size. Hence, the time complexity of this operation is O(n), where n is the size of the list or array being traversed.

for i in numbers:
    print(i)

Space

This function takes a list of elements arr as input and returns a new list with the elements in reverse order. The function creates a new list reversed_arr of the same size as arr to store the reversed elements. The size of reversed_arr depends on the size of the input arr, so the space complexity of this function is O(n). As the input size increases, the amount of memory required to execute the function also increases linearly.

def reverse_list(arr):
    n = len(arr) 
    reversed_arr = [None] * n #create a list of None based on the length or arr
    for i in range(n):
        reversed_arr[n-i-1] = arr[i] #stores the value at the index of arr to the value at the index of reversed_arr starting at the beginning for arr and end for reversed_arr 
    return reversed_arr

print(numbers)
print(reverse_list(numbers))

Quadratic O(n^2)

Time

An example of a quadratic time algorithm is nested loops. When there are two nested loops that both iterate over the same collection, the time taken to complete the algorithm grows quadratically with the size of the collection. Hence, the time complexity of this operation is O(n^2), where n is the size of the collection being iterated over.

for i in numbers:
    for j in numbers:
        print(i,j)

Space

This function takes two matrices matrix1 and matrix2 as input and returns their product as a new matrix. The function creates a new matrix result with dimensions m by n to store the product of the input matrices. The size of result depends on the size of the input matrices, so the space complexity of this function is O(n^2). As the size of the input matrices increases, the amount of memory required to execute the function also increases quadratically.

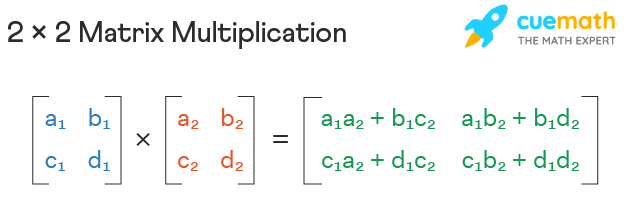
Example of Matrix Multiplication

  • Main take away is that a new matrix is created.
def multiply_matrices(matrix1, matrix2):
    m = len(matrix1) 
    n = len(matrix2[0])
    result = [[0] * n] * m #this creates the new matrix based on the size of matrix 1 and 2
    for i in range(m):
        for j in range(n):
            for k in range(len(matrix2)):
                result[i][j] += matrix1[i][k] * matrix2[k][j]
    return result

print(multiply_matrices([[1,2],[3,4]], [[3,4],[1,2]]))

Logarithmic O(logn)

Time

An example of a log time algorithm is binary search. Binary search is an algorithm that searches for a specific element in a sorted list by repeatedly dividing the search interval in half. As a result, the time taken to complete the search grows logarithmically with the size of the list. Hence, the time complexity of this operation is O(log n), where n is the size of the list being searched.

def binary_search(arr, low, high, target):
    while low <= high:
        mid = (low + high) // 2 #integer division
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            low = mid + 1
        else:
            high = mid - 1

target = 263
result = binary_search(numbers, 0, len(numbers) - 1, target)

print(result)

Space

The same algorithm above has a O(logn) space complexity. The function takes an array arr, its lower and upper bounds low and high, and a target value target. The function searches for target within the bounds of arr by recursively dividing the search space in half until the target is found or the search space is empty. The function does not create any new data structures that depend on the size of arr. Instead, the function uses the call stack to keep track of the recursive calls. Since the maximum depth of the recursive calls is O(logn), where n is the size of arr, the space complexity of this function is O(logn). As the size of arr increases, the amount of memory required to execute the function grows logarithmically.

Exponential O(2^n)

Time

An example of an O(2^n) algorithm is the recursive implementation of the Fibonacci sequence. The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, starting from 0 and 1. The recursive implementation of the Fibonacci sequence calculates each number by recursively calling itself with the two preceding numbers until it reaches the base case (i.e., the first or second number in the sequence). The algorithm takes O(2^n) time in the worst case because it has to calculate each number in the sequence by making two recursive calls.

A visualization of calculating the fibonacci sequence

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

#print(fibonacci(5))
#print(fibonacci(10))
#print(fibonacci(20))
print(fibonacci(30))
#print(fibonacci(40))

Space

This function takes a set s as input and generates all possible subsets of s. The function does this by recursively generating the subsets of the set without the first element, and then adding the first element to each of those subsets to generate the subsets that include the first element. The function creates a new list for each recursive call that stores the subsets, and each element in the list is a new list that represents a subset. The number of subsets that can be generated from a set of size n is 2^n, so the space complexity of this function is O(2^n). As the size of the input set increases, the amount of memory required to execute the function grows exponentially.

def generate_subsets(s):
    if not s:
        return [[]]
    subsets = generate_subsets(s[1:])
    return [[s[0]] + subset for subset in subsets] + subsets

print(generate_subsets([1,2,3]))
#print(generate_subsets(numbers))

Using the time library, we are able to see the difference in time it takes to calculate the fibonacci function above.

  • Based on what is known about the other time complexities, hypothesize the resulting elapsed time if the function is replaced. 
import time

start_time = time.time()
print(fibonacci(34))
end_time = time.time()

total_time = end_time - start_time
print("Time taken:", total_time, "seconds")

start_time = time.time()
print(fibonacci(35))
end_time = time.time()

total_time = end_time - start_time
print("Time taken:", total_time, "seconds")

Hacks

  • Record your findings when testing the time elapsed of the different algorithms.
  • Although we will go more in depth later, time complexity is a key concept that relates to the different sorting algorithms. Do some basic research on the different types of sorting algorithms and their time complexity.

Bubble Sort: Bubble Sort is a simple sorting algorithm that repeatedly steps through the list, compares adjacent elements and swaps them if they are in the wrong order. It has a worst-case and average-case time complexity of O(n^2), where n is the number of elements in the list.

Selection Sort: Selection Sort is an algorithm that repeatedly finds the minimum element from the unsorted part of the list and puts it at the beginning of the list. It has a worst-case and average-case time complexity of O(n^2), where n is the number of elements in the list.

Insertion Sort: Insertion Sort is an algorithm that builds the final sorted array one element at a time. It iterates through the list, comparing each element to its predecessor, and swaps them if they are in the wrong order. It has a worst-case and average-case time complexity of O(n^2), where n is the number of elements in the list.

Merge Sort: Merge Sort is a divide-and-conquer algorithm that divides the input list into two halves, recursively sorts each half, and then merges the two sorted halves into a single sorted list. It has a worst-case and average-case time complexity of O(n log n), where n is the number of elements in the list.

Quick Sort: Quick Sort is another divide-and-conquer algorithm that chooses a pivot element and partitions the list into two sub-lists, according to whether they are less than or greater than the pivot. It then recursively sorts the two sub-lists. It has a worst-case time complexity of O(n^2), but an average-case time complexity of O(n log n), where n is the number of elements in the list.

Heap Sort: Heap Sort is a comparison-based sorting algorithm that uses a binary heap data structure. It has a worst-case and average-case time complexity of O(n log n), where n is the number of elements in the list.

  • Why is time and space complexity important when choosing an algorithm?

Time and space complexity is important when choosing an algorithm because you want to make sure that the algorithm you are choosing is the most efficient in both the space and time aspect. Space and time can also affect how readible your algorithm is which is also an important factor.

  • Should you always use a constant time algorithm / Should you never use an exponential time algorithm? Explain?

There is no specific always or never in these alogirthms. When choosing an algorithm you should choose what is the most efficient for you. An example of a constant time algorithm is accessing a specific element in an array or a dictionary. The time it takes to access the element does not depend on the size of the array or dictionary, but only on the time it takes to perform a single memory access. An example of an exponential time algorithm is the brute force approach to solving the traveling salesman problem. The brute force approach involves trying every possible permutation of cities to find the shortest route. As the number of cities increases, the number of permutations grows exponentially, making the algorithm impractical for large datasets.

  • What are some general patterns that you noticed to determine each algorithm's time and space complexity?

Data structures: Analyze the data structures used in the algorithm and how they grow with the input size. For example, if the algorithm uses an array that doubles in size with each addition, it has O(n) space complexity.

Nested loops: Look for nested loops in the code and analyze how many times they run based on the input size. Nested loops that iterate over the entire input for each level can indicate O(n^2), O(n^3), or higher time complexity.

Recursion: Recursive functions can be analyzed by looking at the number of times the function is called and the size of the input for each call. Recursive functions that call themselves multiple times with a smaller input size can be an indicator of exponential time complexity.

Complete the Time and Space Complexity analysis questions linked below. Practice

  • What is the time, and space complexity of the following code: 
import random

a = 0
b = 0
for i in range(N):
  a = a + random()
 
for i in range(M):
  b= b + random()
  1. O(N * M) time, O(1) space
  2. O(N + M) time, O(N + M) space
  3. O(N + M) time, O(1) space
  4. O(N * M) time, O(N + M) space

The answer to this question is 3. O(N) is the first loop and O is the second loop.(M). We are unable to determine which word is the leading one because N and M are independent variables. As a result, the given problem's time complexity will be O(N+M). Space Complexity will be constant or O since the size of the variables does not rely on the size of the input.(1)

  • What is the time complexity of the following code: 
a = 0;
for i in range(N):
for j in reversed(range(i,N)):
	a = a + i + j;
  1. O(N)
  2. O(N*log(N))
  3. O(N * Sqrt(N))
  4. O(N*N)

The answer to this question is 4.

The above code runs total no of times

= N + (N – 1) + (N – 2) + … 1 + 0

= N * (N + 1) / 2

= 1/2 N^2 + 1/2 N

O(N^2) times.

  • What is the time complexity of the following code: 
k = 0;
for i in range(n//2,n):
  for j in range(2,n,pow(2,j)):
        k = k + n / 2;
  1. O(n)
  2. O(N log N)
  3. O(n^2)
  4. O(n^2Logn)

The answer to this question is 2. I don't know how to do logarithms.

  • What does it mean when we say that an algorithm X is asymptotically more efficient than Y?
  1. X will always be a better choice for small inputs
  2. X will always be a better choice for large inputs
  3. Y will always be a better choice for small inputs
  4. X will always be a better choice for all inputs

The answer to this question is 2. This is because X is more efficient than Y which means that X will be better for larger inputs.

  • What is the time complexity of the following code:
a = 0
i = N
while (i > 0):
  a += i
  i //= 2
  1. O(N)
  2. O(Sqrt(N))
  3. O(N / 2)
  4. O(log N)

The answer to this question is 4 because we have to find the smallest x such that ‘(N / 2^x )< 1 OR 2^x > N’ x = log(N)

  • Which of the following best describes the useful criterion for comparing the efficiency of algorithms?
  1. Time
  2. Memory
  3. Both of the above
  4. None of the above

The answer is 3 both because for efficiency time and memory must be considered

  • How is time complexity measured?
  1. By counting the number of algorithms in an algorithm.
  2. By counting the number of primitive operations performed by the algorithm on a given input size.
  3. By counting the size of data input to the algorithm.
  4. None of the above

The answer to this is 2 beecause the input size will control the amount of time that it will take because of the number of operations

  • What will be the time complexity of the following code?
for i in range(n):
  i=i*k
  1. O(n)
  2. O(k)
  3. O(logkn)
  4. O(lognk)

The answer is 3 because loops for the kn-1 times, so after taking log it becomes logkn.

  • What will be the time complexity of the following code?
value = 0;
for i in range(n):
  for j in range(i):
    value=value+1
  1. n
  2. (n+1)
  3. n(n-1)
  4. n(n+1)

The answer is 3 because the for loop will run for (n) times and another for loop will be run for (n-1) times as the inner loop will only run till the range i which is 1 less than n , so overall time will be n(n-1).

  • Algorithm A and B have a worst-case running time of O(n) and O(logn), respectively. Therefore, algorithm B always runs faster than algorithm A.
  1. True
  2. False

The answer is false because the Big-O notation provides an asymptotic comparison in the running time of algorithms. For n < n0​​, algorithm A might run faster than algorithm B, for instance.